learning deformable object dynamics
interpretible models for predicting deformable linear object dynamics
Introduction
Modeling deformable objects presents a significant challenge for the robotics community. Current methodologies have primarily tackled quasi-static scenarios. This study centers on capturing the complex nonlinear dynamics of deformable linear objects—such as cables, ropes, and rods—from partial observations. Below, we present an illustrative example demonstrating the typical motions we aim to predict.

At a high level, our work addresses the following problem: given measurements of positions, velocities and accelerations of one end of a deformable object, predict the position and velocity of the other end over time.
Proposed method
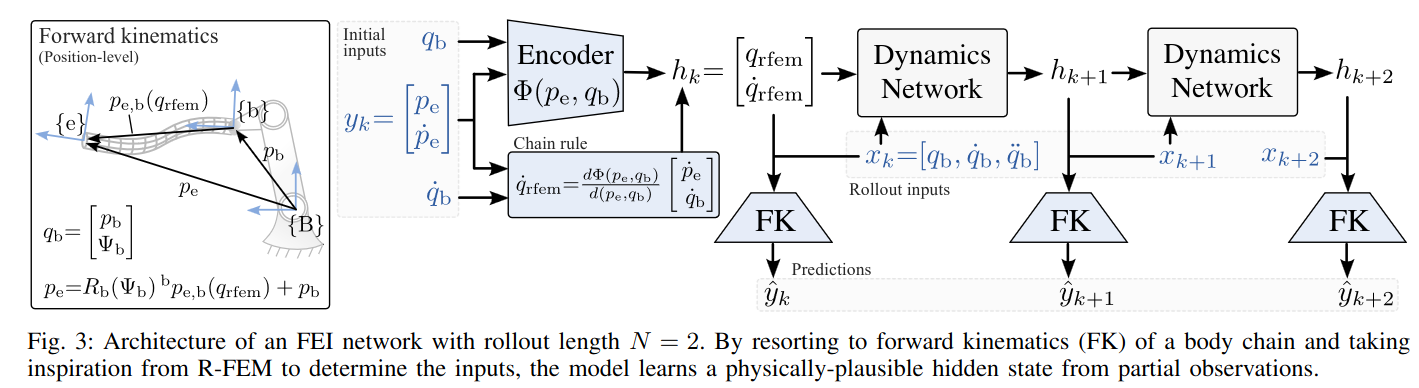
We propose an interpretable method employing an encoder-dynamics-decoder architecture. To elaborate:
- state representation we leverage a state representation of lumped parameter modeling approach called pseudo-rigid body method;
- encoder reconstructs hidden states \(h_k\) from partial observations \(y_k\) and controlled inputs \(x_k\);
- dynamics unrolls hidden states over time based on controlled inputs \(x_k, x_{k+1},\dots,x_{k+N}\);
- decoder maps hidden states and inputs into observartions.’
The proposed method named PRB-Net is visualized below.
Results
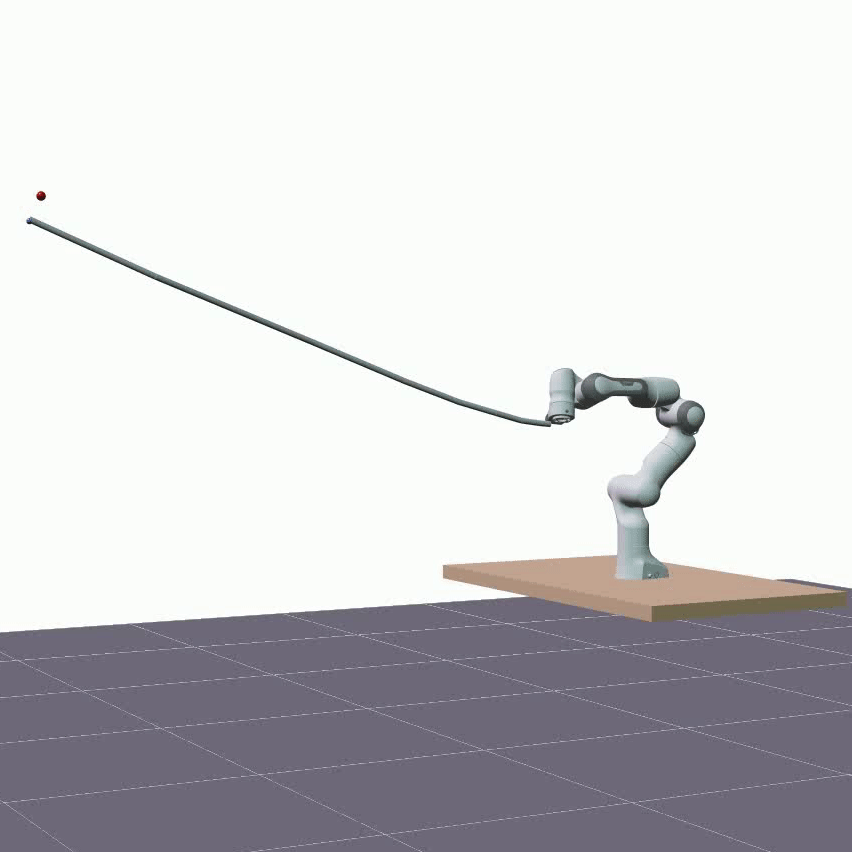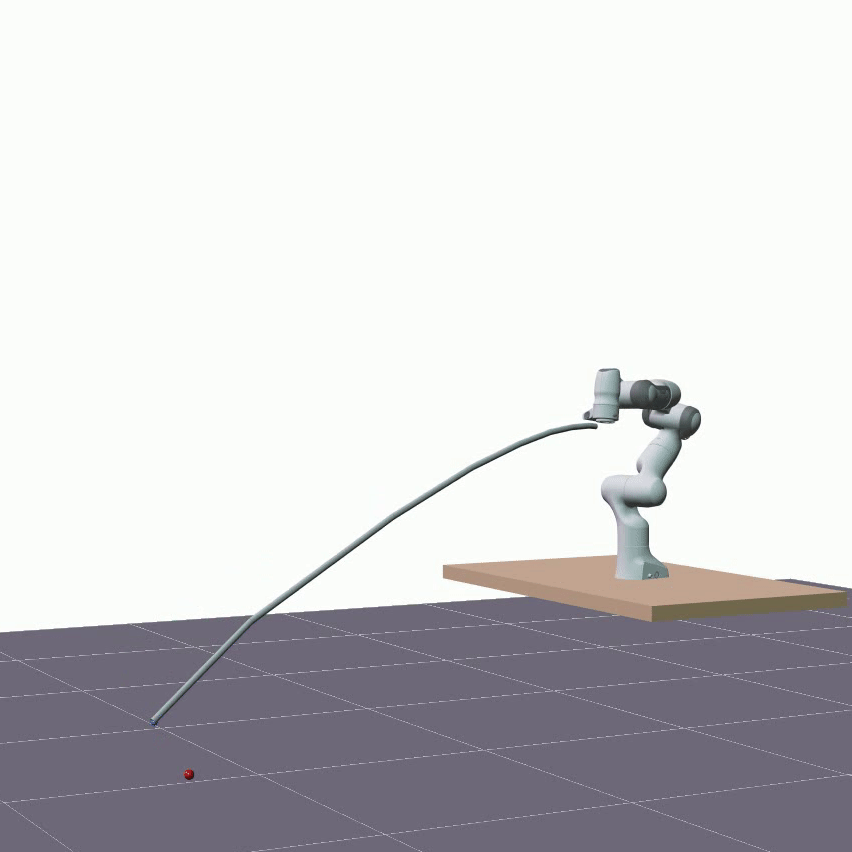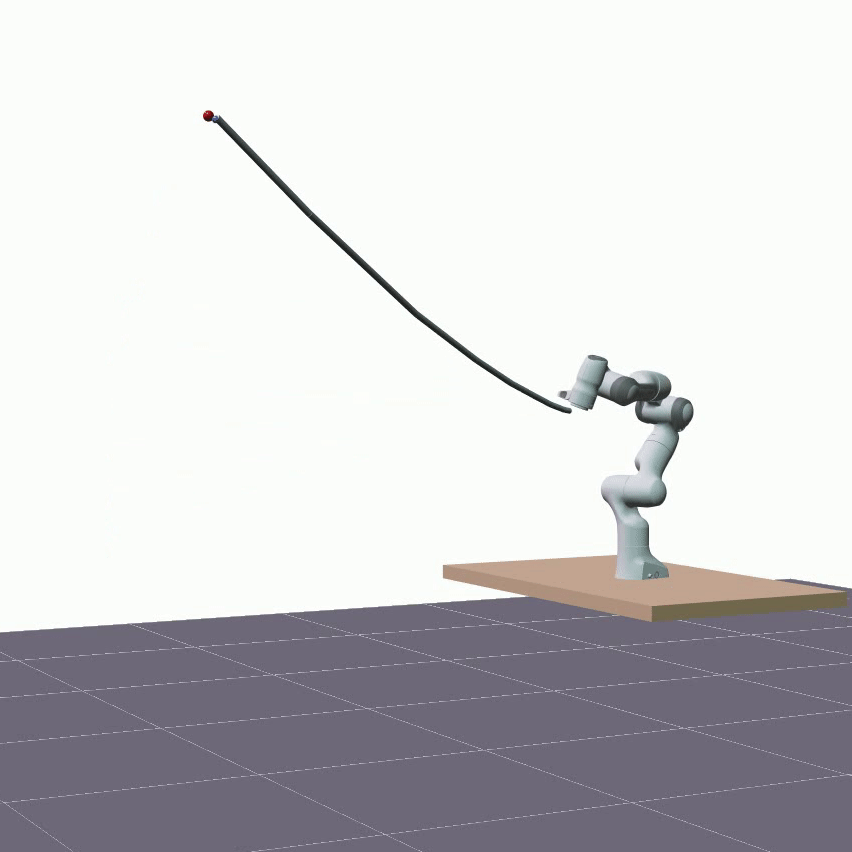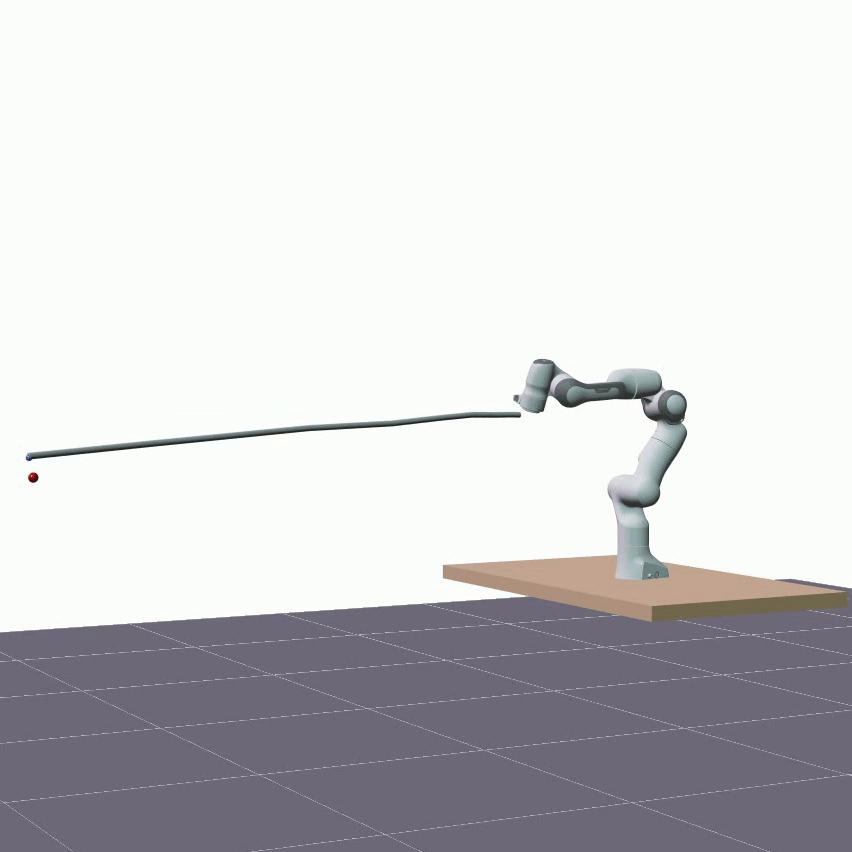
The visualizations below showcase predictions made on test data, employing the same rollout length as utilized during training, specifically 1 second. The two DLOs under consideration are a 1.92m aluminum rod and a 1.9m foam cylinder. The red sphere represents the actual measured position of the DLO’s end. The overall shape of a DLO is reconstructed from hidden states using the proposed forward kinematics decoder.

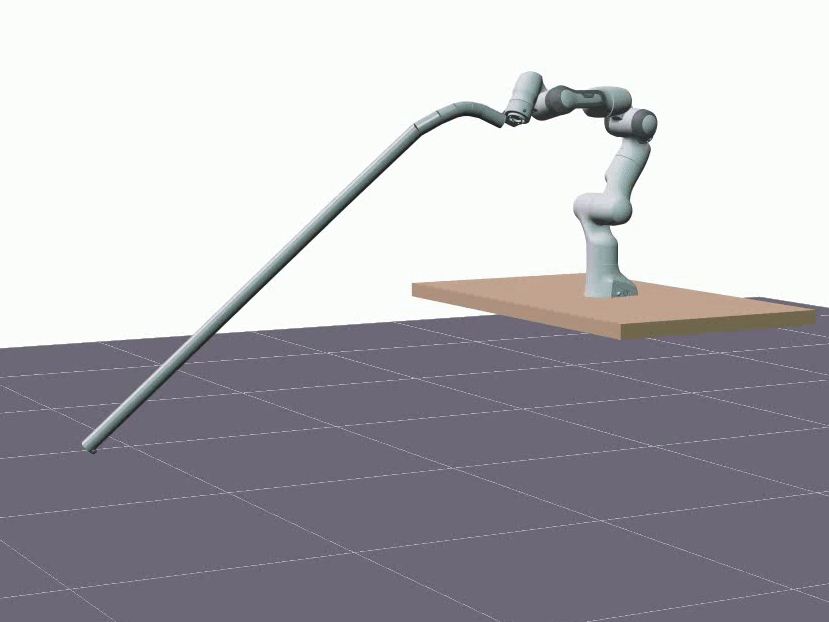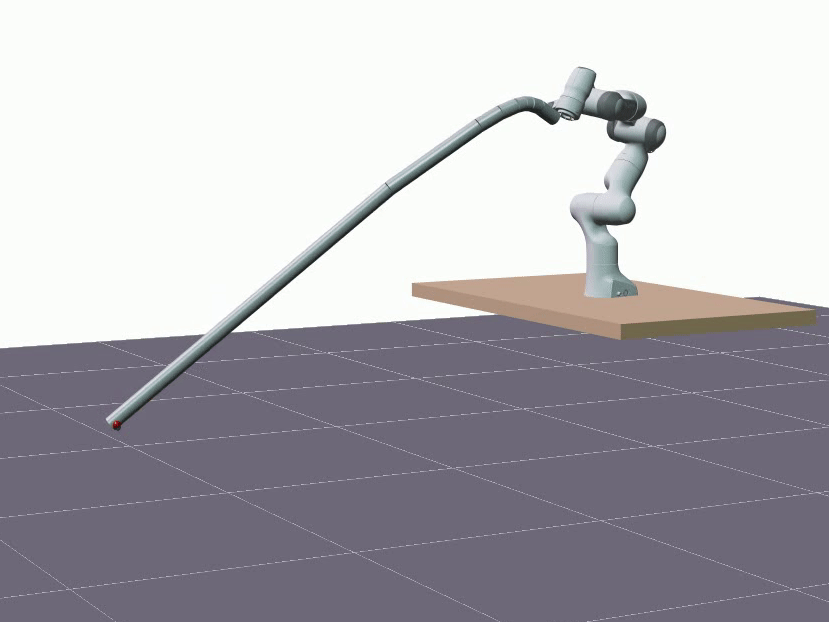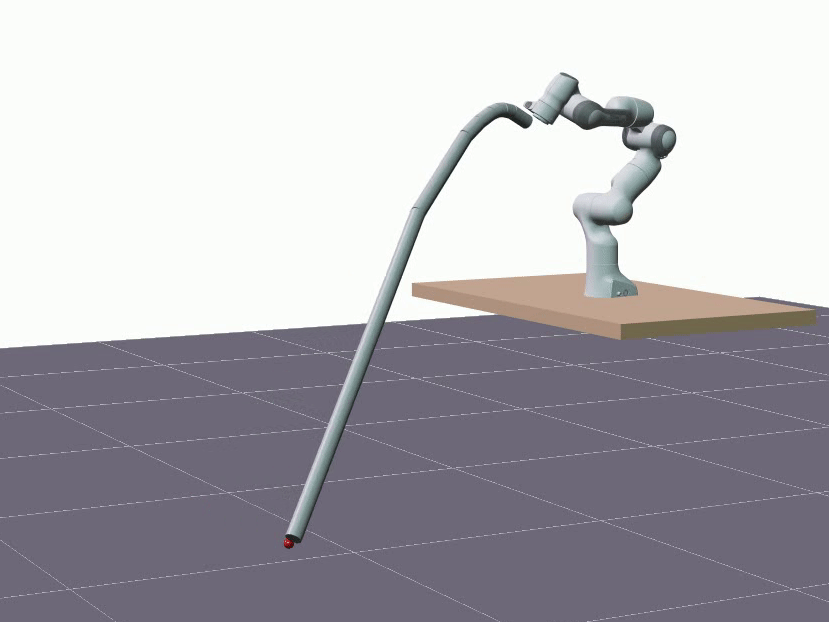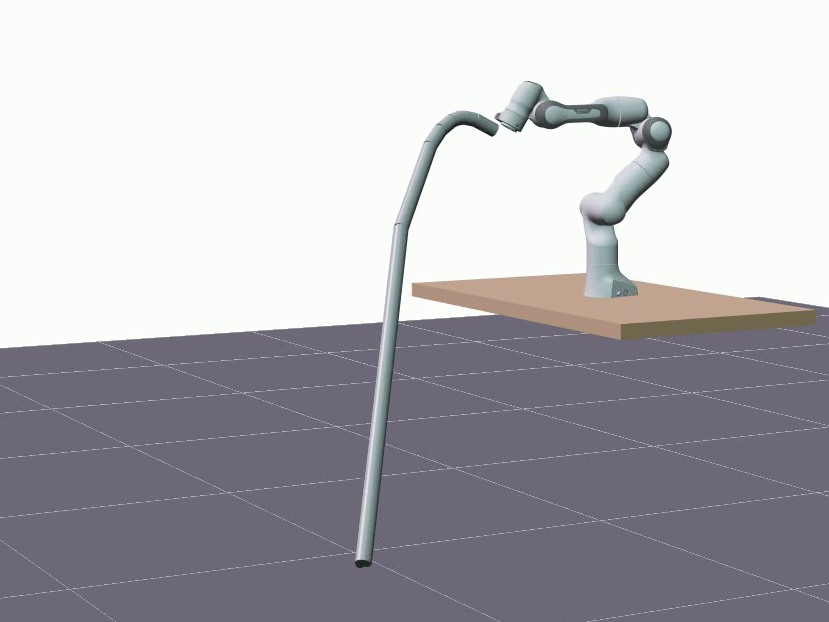

Furthermore, we evaluated the proposed model’s ability to generalize in terms of longer predictions. The visualizations below showcase predictions spanning a duration of 5 seconds.
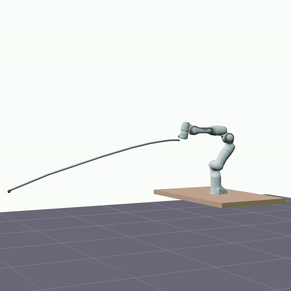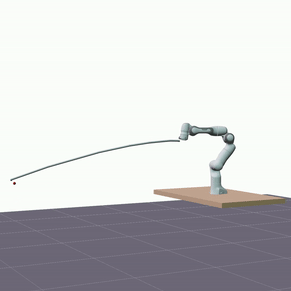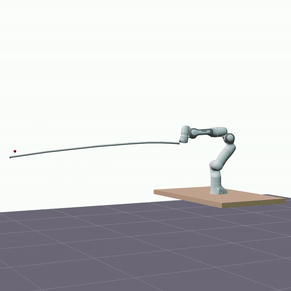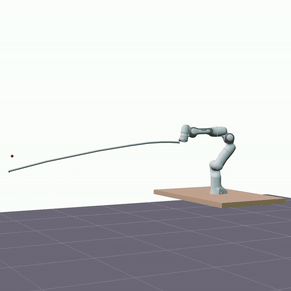
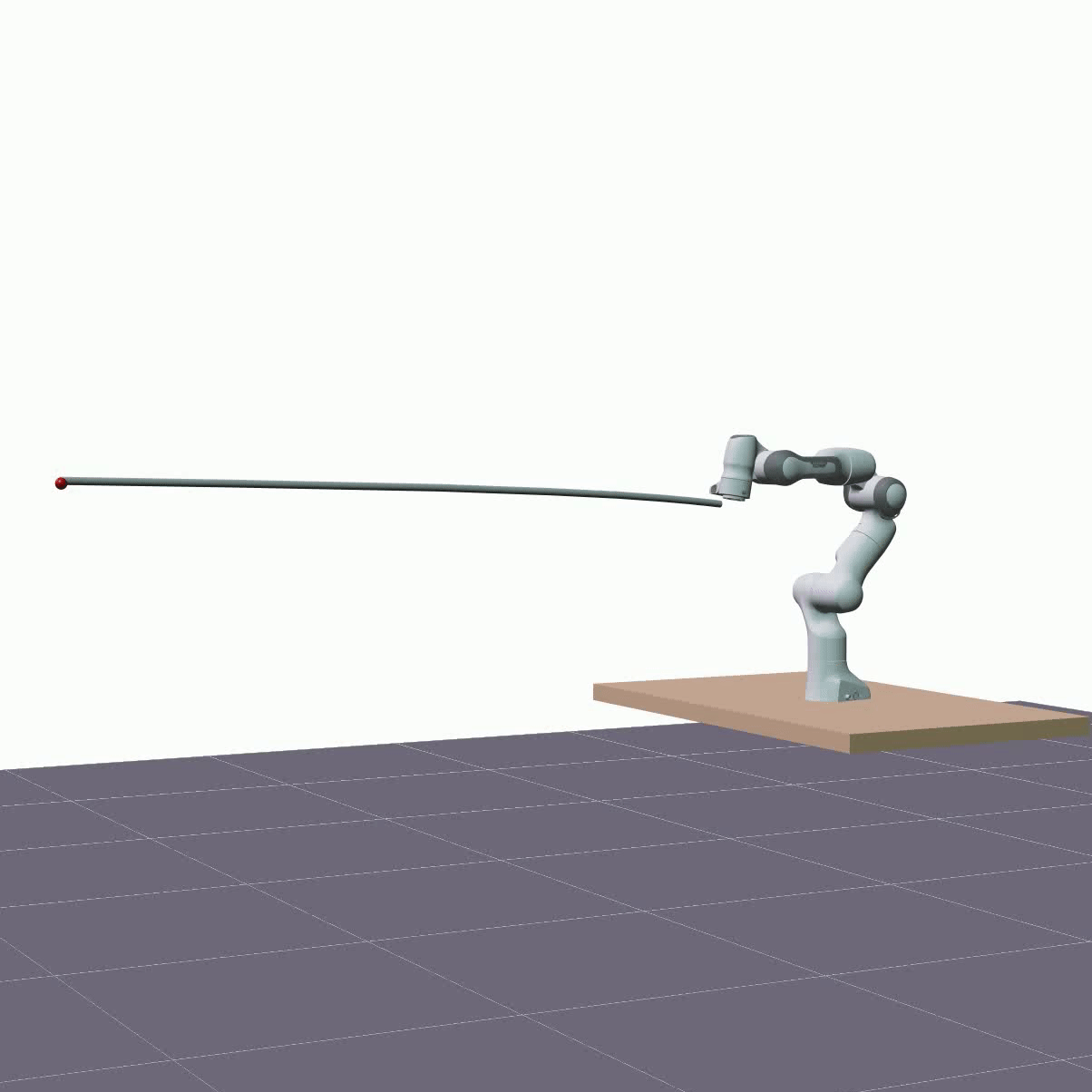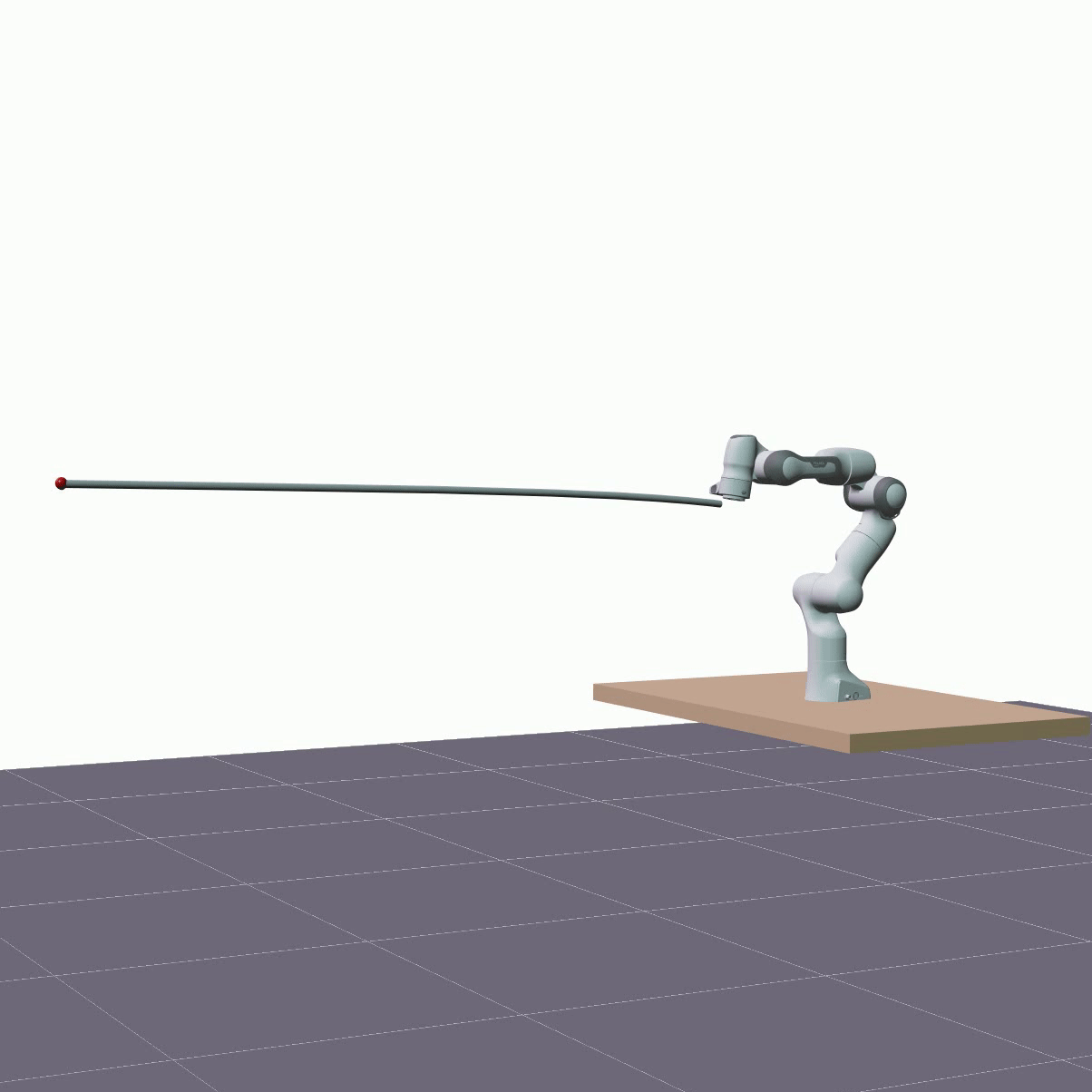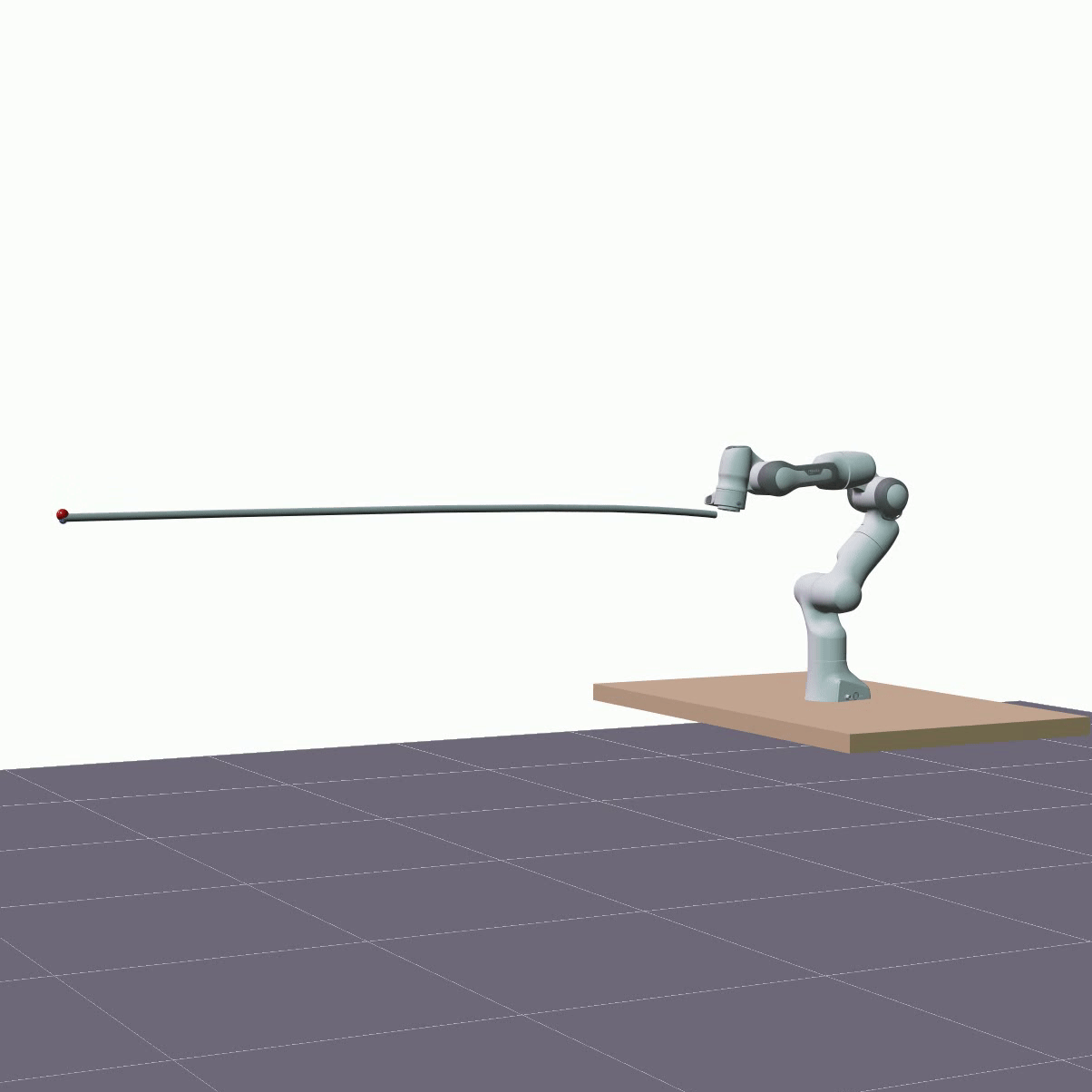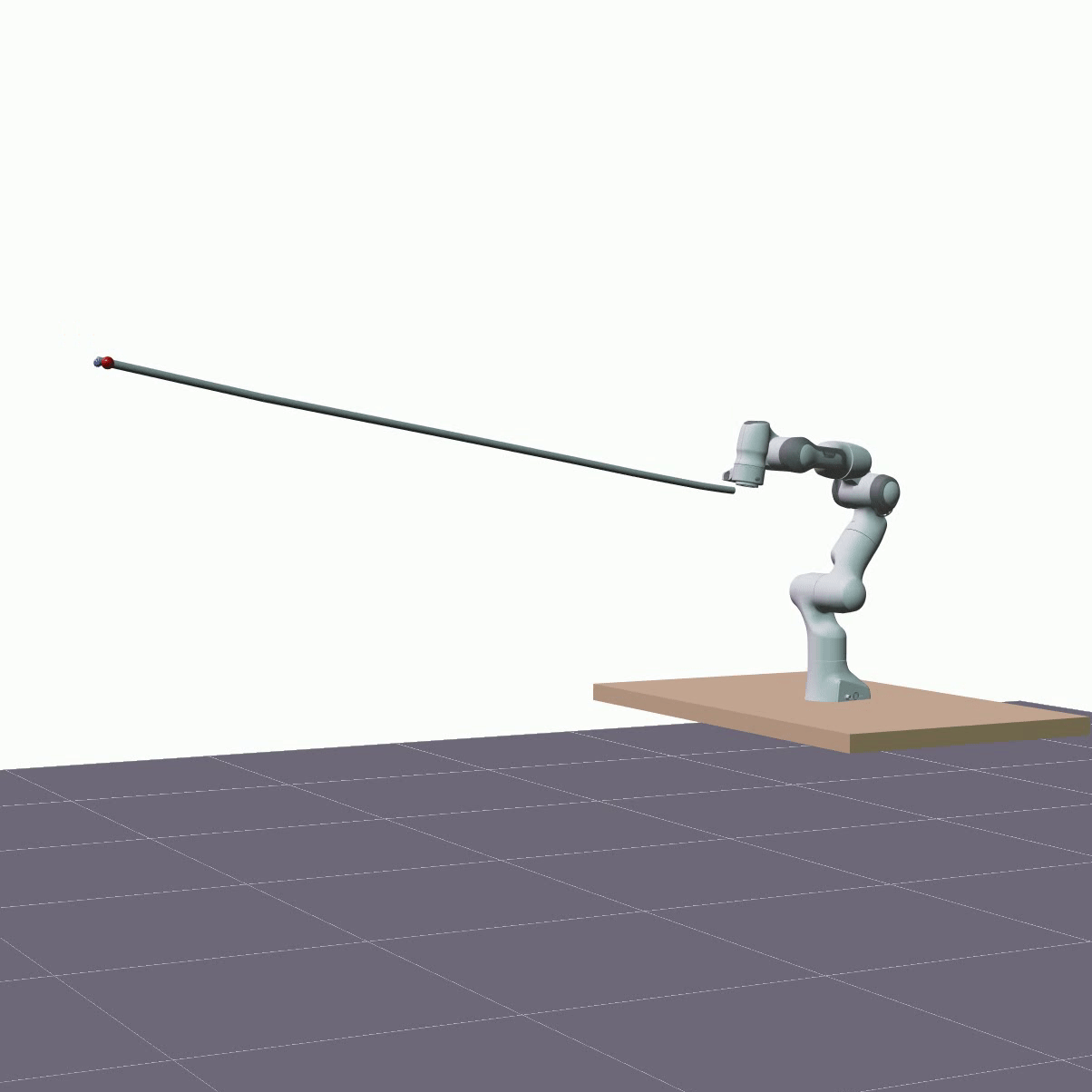
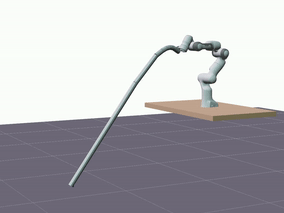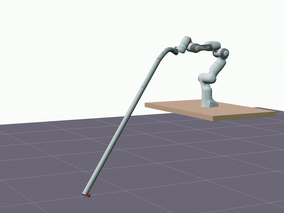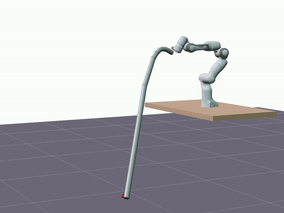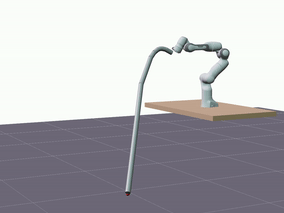
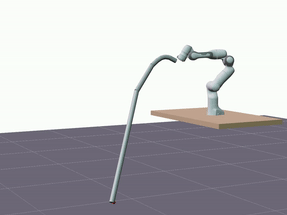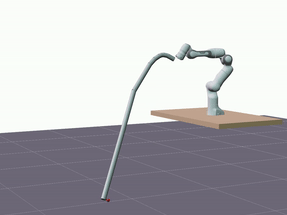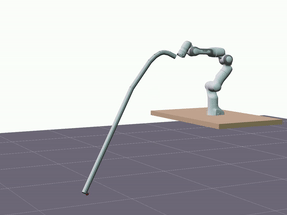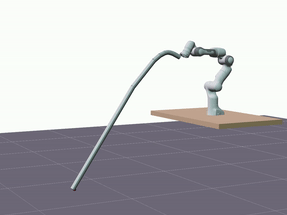
Despite a decrease in the model’s accuracy, it consistently maintains reasonable precision—below 10 cm—and does not diverge.
References
Mamedov, S., Geist, A.R., Swevers, J. and Trimpe, S., 2023. Finite element inspired networks: Learning physically-plausible deformable object dynamics from partial observations. arXiv preprint arXiv:2307.07975.